二叉查找树
二叉查找树定义
二叉查找树 (Binary Search Tree) 是按照平衡顺序排列的二叉树, 也称二叉搜索树、 有序二叉树(ordered binary tree),排序二叉树(sorted binary tree)。
首先, 要符合二叉树的特性:
- 可以为空;
- 也可以拥有连个互不相交的子树, 即: 左子树和右子树。
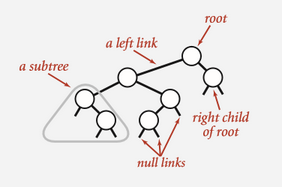
平衡排序, 每个节点都有一个 key, 并且每个节点的 key 都符合:
- 大于左子树中所有节点的 key;
- 小于右子树所有节点的 key ;
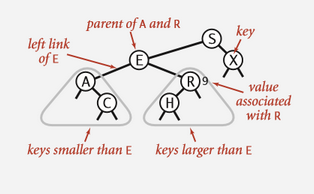
二叉查找树节点必须包含四个字段:
- 一个
Key和一个Value; - 对左子树和右子树的引用;
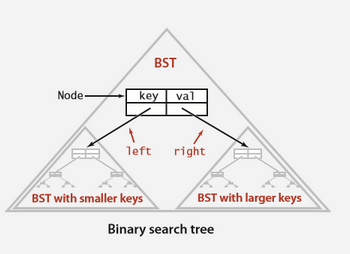
对应的 C# 代码实现如下:
class Node {
public TKey Key;
public TValue Val;
public Node Left, Right;
}
上面的代码中, TKey 和 TValue 是泛型类型, TKey 必须实现 IComparable<TKey>
接口, 用于比较两个 TKey 实例的大小。
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n) 。
二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、multiset、关联数
组等。
二叉查找树常用操作
二叉查找树必须引用根节点, 定义如下:
public class BST<TKey, TValue> where TKey : IComparable<TKey> {
private Node root;
}
查找
既然是二叉查找树, 查找操作肯定要先实现了, 二叉查找树查找的思路是:
- 从根节点开始查找, 对于任意节点:
- 如果该节点为 null , 则返回空值或者该类型的默认值, 表示找不到;
- 将节点的 key 与要查找的 key 进行比较;
- 如果要查找的 key 小于节点的 key , 则继续查找该节点的左子树;
- 如果要查找的 key 大于节点的 key , 则继续查找该节点的右子树;
- 如果相等, 表示已经找到, 返回该节点的值。
对应的 C# 代码实现如下:
public TValue Get(TKey key) {
return Get(root, key);
}
private TValue Get(Node x, TKey key) {
if (x == null) {
return default(TValue);
}
int cmp = key.CompareTo(x.Key);
if (cmp < 0) {
return Get(x.Left, key);
}
if (cmp > 0) {
return Get(x.Right, key);
}
return x.Val;
}
添加
添加操作与查找操作类似, 如果能够在树中找到 key 对应节点, 则设置节点的值, 如果 找不到, 则返回一个新的节点, 实现代码如下:
public void Put(TKey key, TValue val) {
root = Put(root, key, val);
}
private Node Put(Node x, TKey key, TValue val) {
if (x == null) {
return new Node {
Key = key, Val = val, N = 1
};
}
int cmp = key.CompareTo(x.Key);
if (cmp < 0) {
x.Left = Put(x.Left, key, val);
}
else if (cmp > 0) {
x.Right = Put(x.Right, key, val);
}
else {
x.Val = val;
}
x.N = 1 + Size(x.Left) + Size(x.Right);
return x;
}
删除
从二叉查找树中删除指定的节点稍微复杂一点, 要分下面三种情况:
1 删除最小 Key 节点
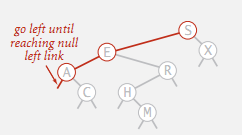
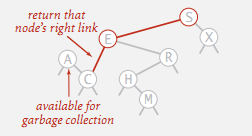
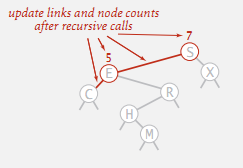
要删除二叉查找树的最小 key 节点:
- 查找当前结点的左节点, 直到找到一个左节点为空的节点;
- 将该节点替换为该节点的右节点;
 |
 |
 |
对应的 C# 代码实现代码如下:
public void DeleteMin() {
root = DeleteMin(root);
}
private Node DeleteMin(Node x) {
if (x.Left == null) {
return x.Right;
}
x.Left = DeleteMin(x.Left);
x.N = Size(x.Left) + Size(x.Right) + 1;
return x;
}
2 删除最大 key 节点
删除最大 key 节点的思路与删除最小 key 节点的思路类似, 查找节点的右节点即可, 对 应的 C# 实现代码如下:
public void DeleteMax() {
root = DeleteMax(root);
}
private Node DeleteMax(Node x) {
if (x.Right == null) {
return x.Left;
}
x.Right = DeleteMax(x.Right);
x.N = Size(x.Left) + Size(x.Left) + 1;
return x;
}
3 删除任意 key 节点
要从二叉查找树中删除 key 为 k 的节点, 假设树中找到的节点为 t , 要分下面几
种情况:
如果节点 t 没有子节点, 将节点 t 的父节点指向 t 的引用设置为空即可;
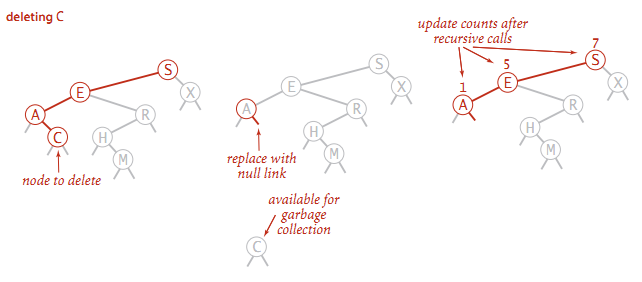
节点 t 的右节点或左节点为空, 则用 t 的另一个节点替换掉 t 即可;
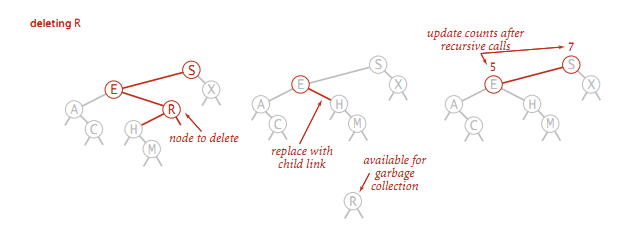
节点 t 的左右节点均不为空, 则需要从 t 的右节点开始找到并删除最小的节点 x ,
并用节点 x 替换 t 的位置;
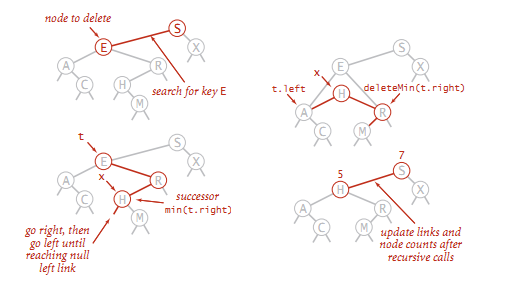
实现代码如下:
public void Delete(TKey key) {
root = Delete(root, key);
}
private Node Delete(Node x, TKey key) {
if (x == null) {
return null;
}
int cmp = key.CompareTo(x.Key);
if (cmp < 0) {
x.Left = Delete(x.Left, key);
}
else if (cmp > 0) {
x.Right = Delete(x.Right, key);
}
else {
if (x.Right == null) {
return x.Left;
}
if (x.Left == null) {
return x.Right;
}
Node t = x;
x = Min(t.Right);
x.Right = DeleteMin(t.Right);
x.Left = t.Left;
}
x.N = Size(x.Left) + Size(x.Right) + 1;
return x;
}
二叉查找树最终可能的形状如下图所示:
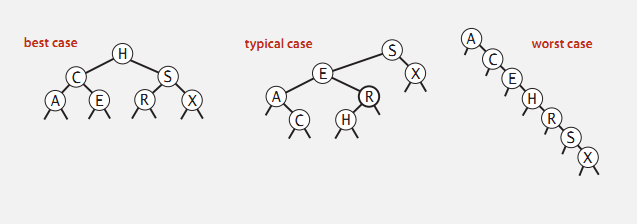
在实际算法中, 应避免最差情况, 因为在这种情况下, 二叉树退化成链表, 查找操作的
速度由 O(LogN) 降为 O(N) 就完全没有意义了。